Contents
EJERCICIO 1
Imprimir una tabla formateada (entero y real) del logaritmo natural de los números 10, 20, 40, 60, y 80.
x = [10 20 40 60 80 100]'; y = [x log(x)]; fprintf('Numero\tln(Numero) \n') fprintf('%5d \t %.4f \n', y')
Numero ln(Numero) 10 2.3026 20 2.9957 40 3.6889 60 4.0943 80 4.3820 100 4.6052
EJERCICIO 2
Calcular IMC
% El código de la función es: % while 1 % est = input('Ingrese su estatura en metros: '); % peso = input('Ingrese su peso en kg: '); % % imc=peso/(est^2); % % if imc <16 % fprintf('Infrapeso: Delgadez Severa') % elseif (imc<17 & imc>16) % fprintf('Infrapeso: Delgadez moderada') % elseif (imc<18.5 & imc>17) % fprintf('Infrapeso: Delgadez aceptable') % elseif (imc<25 & imc>18.5) % fprintf('Peso normal') % elseif (imc<30 & imc>25) % fprintf('Sobrepeso') % elseif (imc<35 & imc>30) % fprintf('Obeso: Tipo I') % elseif (imc<40 & imc>35) % fprintf('Obeso: Tipo II') % elseif (imc>40) % fprintfn % ('Obeso: Tipo III') % end % % mensaje=input('Desea continuar (s/n): ') % if mensaje==n % break % else % continue % end % end

EJERCICIO 3
Cambio de base
% u=input('¿En qué base quiere(2-16):? '); % v=input('Dime un número decimal: '); % a=dec2base(v,u); % disp(a)

EJERCICIO 4
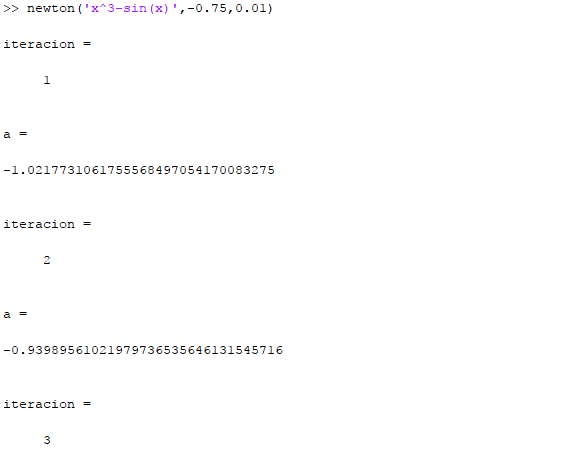
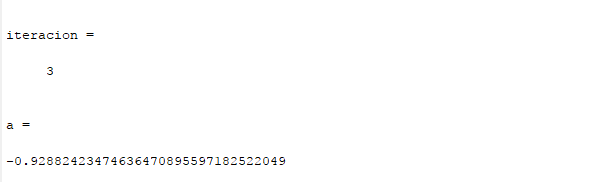
Función Newton
% El código de la función es: % function y=newton(fun,x0,tol) % dfun=diff(sym(fun)); % f=subs(fun,x0); % df=subs(dfun,x0); % iteracion=1; % while abs(f)>tol % a=vpa(x0-f/df); % f=subs(fun,a); % df=subs(dfun,a); % x0=a; % iteracion % a % iteracion=iteracion+1; % end % end
EJERCICIO 5
Calcular valores de calor y temperaturas incógnitas
A=[100 0 0 0 -1 1 0;0 200 0 0 0 -1 1; 0 0 50 0 -1 0 0; 0 0 0 100 0 -1 0; 0 300 0 0 0 0 -1;1 0 1 0 0 0 0;1 -1 0 -1 0 0 0]; B=[0 0 -50 -50 -50 25 0]; X=A/B; % Calores Q1=X(1) Q2=X(2) Q3=X(3) Q4=X(4) % Temperaturas Tc=X(5) Tp=X(6) Tw=X(7)
Q1 =
0.0092
Q2 =
-0.0031
Q3 =
-0.3015
Q4 =
-0.6185
Tc =
0
Tp =
-0.0062
Tw =
0.0062
EJERCICIO 6
Para la matriz de coeficientes anterior hallar el número de condición, las normas 1,2, Inf y frobenius, la factorización LU, es decir A = LU y aplicar a continuación X = U-1L-1b para resolver el sistema anterior.
% Matriz A=[100 0 0 0 -1 1 0;0 200 0 0 0 -1 1; 0 0 50 0 -1 0 0;0 0 0 100 0 -1 0; 0 300 0 0 0 0 -1;1 0 1 0 0 0 0;1 -1 0 -1 0 0 0] B=[0;0;-50;-50;-50;25;0] % Número de condición condicion=cond(A) % Norma 1 norma1=norm(A,1) % Norma 2 norma2=max(svd(A)) % Infinito normainf=norm(A,inf) % Frobenius frobenius=norm(A,'fro') % Factorización LU [L U]=lu(A)
A =
100 0 0 0 -1 1 0
0 200 0 0 0 -1 1
0 0 50 0 -1 0 0
0 0 0 100 0 -1 0
0 300 0 0 0 0 -1
1 0 1 0 0 0 0
1 -1 0 -1 0 0 0
B =
0
0
-50
-50
-50
25
0
condicion =
2.6488e+04
norma1 =
501
norma2 =
360.5570
normainf =
301
frobenius =
390.5278
L =
1.0000 0 0 0 0 0 0
0 0.6667 0 0 0 1.0000 0
0 0 1.0000 0 0 0 0
0 0 0 1.0000 0 0 0
0 1.0000 0 0 0 0 0
0.0100 0 0.0200 0 1.0000 0 0
0.0100 -0.0033 0 -0.0100 0.3333 0.0167 1.0000
U =
100.0000 0 0 0 -1.0000 1.0000 0
0 300.0000 0 0 0 0 -1.0000
0 0 50.0000 0 -1.0000 0 0
0 0 0 100.0000 0 -1.0000 0
0 0 0 0 0.0300 -0.0100 0
0 0 0 0 0 -1.0000 1.6667
0 0 0 0 0 0 -0.0311
EJERCICIO 7
Hallar los autovalores y autovectores de la matriz A:
% Introduzco la matriz A=[0 1 -1; -6 -11 6; -6 -11 5]; % Calculo autovalores y autovectores [autovectores autovalores]=eig(A)
autovectores =
0.7071 -0.2182 -0.0921
0.0000 -0.4364 -0.5523
0.7071 -0.8729 -0.8285
autovalores =
-1.0000 0 0
0 -2.0000 0
0 0 -3.0000
EJERCICIO 8
Para el siguiente circuito, determinar los voltajes de los nodos V1 y V2 y la potencia entregada por cada fuente:
A=[1.5-2j -0.35+1.2j; -0.35+1.2j 0.9-1.6j]; B=[30+40j; 20+15j]; disp('Voltajes: ') V=A\B; V1=V(1) V2=V(2) disp('Potencias: ') S=V.*conj(B); S1=S(1) S2=S(2)
Voltajes: V1 = 3.5902 +35.0928i V2 = 6.0155 +36.2212i Potencias: S1 = 1.5114e+03 + 9.0918e+02i S2 = 6.6363e+02 + 6.3419e+02i
EJERCICIO 9
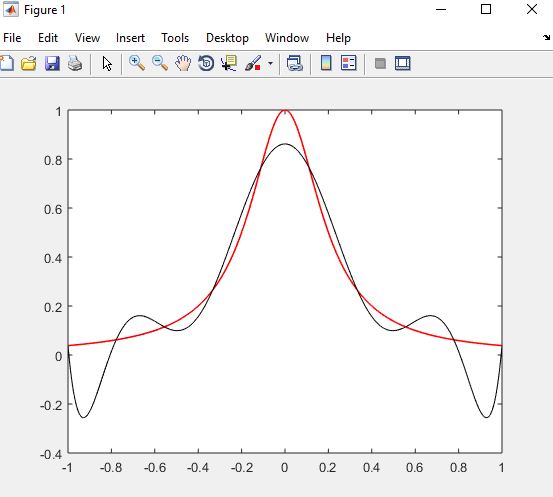
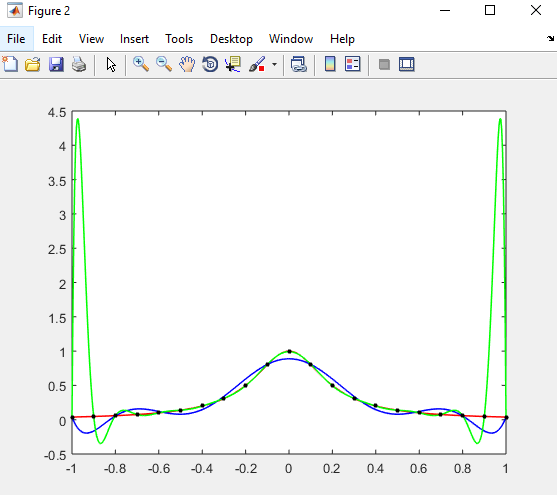
Desarrollar una función de interpolación Lagrange
% El código de la función es: % function lagrange() % % Apartado a % % f=@(x) 1./(1 + 25*x.^2); % @: handle % x = linspace(-1,1,500); % Creo el rango [-1,1] 500 puntos, para graficar % y_true=f(x); % figure; % plot(x,y_true,'r','linewidth',1); % hold on; % % % N = 10; % 10 puntos equidistantes % xint = linspace(-1,1,N); % yint = zeros(1,N); % y=f(xint); % n1=length(x); % tamaño del vector % for i = 1:n1; % yint(i) = LagrangeINT(xint,y,x(i)); % Invocamos la función % end % plot(x,yint,'k'); % hold on; % % % Apartado b % % f=@(x) 1./(1 + 25*x.^2); % @: handle % x = linspace(-1,1,500); % Creo el rango [-1,1] 500 puntos, para graficar % y_true=f(x); % figure; % plot(x,y_true,'r','linewidth',1); % hold on; % % % % N = 10; % xdata = linspace(-1,1,N+1); % ydata = f(xdata); % p = polyfit(xdata,ydata,N-1) % y_fit = polyval(p,x); % poly_10 = plot(x,y_fit,'b','linewidth',1); % hold on; % plot(xdata,ydata,'k.','markersize',12); % hold on; % % % % Apartado c % % N = 20; % xdata=linspace(-1,1,N+1); % ydata = f(xdata); % p = polyfit(xdata,ydata,N-1) % y_fit = polyval(p,x); % poly_20 = plot(x,y_fit,'g','linewidth',1); % hold on; % plot(xdata,ydata,'k.','markersize',12); % hold on; % end % % % function Yint = LagrangeINT(x,y,Xint) % La función igual al nombre del fichero % n = length(x) % L = ones(1,n); % for i = 1:n % L(i)=1; % for j = 1:n % if j ~= i % L(i)=L(i)*(Xint-x(j))/(x(i)-x(j)); % end % end % % Yint=Yint+y(i)*L % end % Yint=sum(y.*L); % end
EJERCICIO 10
Fichero Excel [x,y,z,t]=xlsread('winddata.xlsx','A2:D78877');
EJERCICIO 11
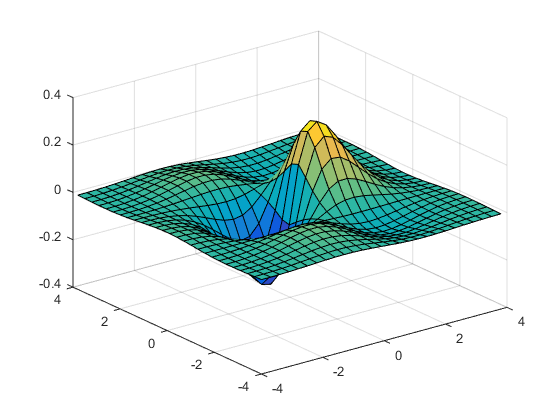
Graficar la curva para un intervalo de -4 a 4 en pasos de 0.3
x=-4:0.3:4;
y=x;
[A B]=meshgrid(x,y);
X=sin(A).*cos(B).*exp(-(A.^2+B.^2).^0.5);
% Dibujamos la curva
surf(A,B,X)
EJERCICIO 12
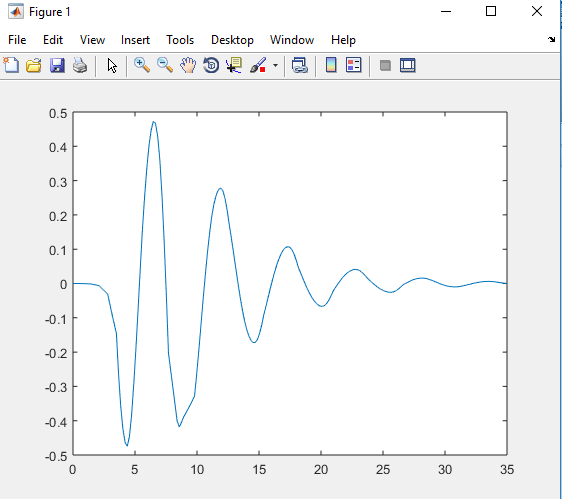
Resolver la ec. diferencial
% Establecemos condiciones iniciales % y0=1; % dy0=0; % k=0.15; % t0=0; % tf=35; % Calculamos la solución %[t yy]=ode45(@funcionde,[t0 tf],[y0 dy0],[],k) % La función y(t) es %yt=yy(:,1) % n=length(yt) % plot(linspace(0,35,n),yt) % Derivada de dy(t)/dt: %dyt=yy(:,2) %plot(linspace(0,35,n),dyt) % El código de la función es: % function y=funcionde(t,y,z); % h=sin(pi*t/5).^(t<=5); % y=[y(2);-2*z*y(2)-y(1)+h]; % end
EJERCICIO 13
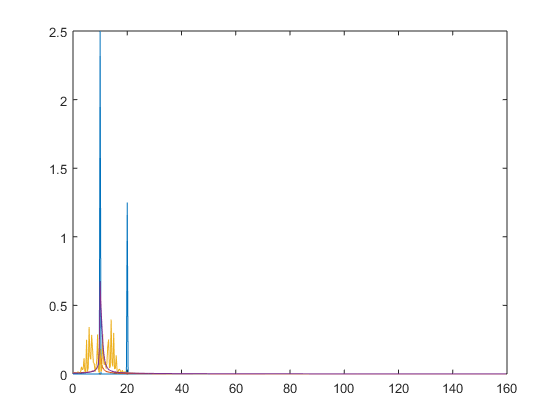
Tomando como base las condiciones del ejemplo de la transformada de Fourier de los apuntes (pág. 124), graficar para las siguientes señales la gráfica de la señal en el tiempo y la gráfica de la amplitud espectral en función de la frecuencia:
% Valores k=5; m=10; fo=10; Bo=2.5; N=2^m; T=2^k/fo; t=(0:N-1)*T/N; df=(0:N/2-1)/T; % Gráfica 1 g = Bo*sin(2*pi*fo*t)+Bo/2*sin(2*pi*fo*2*t); An = abs(fft(g, N))/N; plot(df, 2*An(1:N/2)) hold on % Gráfica 2 g = exp((-2).*t).*sin(2*pi*fo*t); An = abs(fft(g, N))/N; plot(df, 2*An(1:N/2)) hold on % Gráfica 3 g = sin(2*pi*fo*t+5*sin(2*pi*fo*t/10)); An = abs(fft(g, N))/N; plot(df, 2*An(1:N/2)) hold on % Gráfica 4 g = sin(2*pi*fo*t-5*exp(-2*t)); An = abs(fft(g, N))/N; plot(df, 2*An(1:N/2)) hold on
EJERCICIO 14
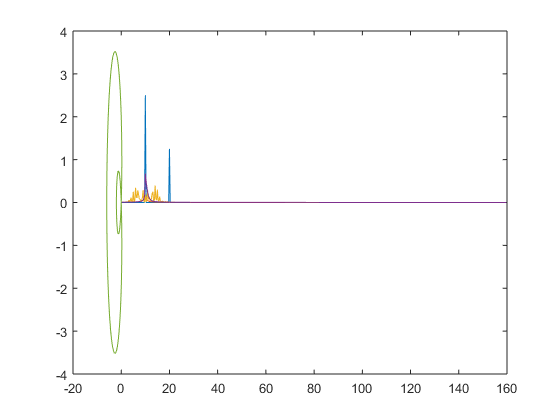
Graficar la siguiente función curva en coordenadas polares :
% Función e intervalo f=inline('2-4.*cos(t)'); i=linspace(-pi,pi,150); % Gráfica polar(i,f(i))
EJERCICIO 15
Ejercicio de una catenaria
% Parámetros: w=10; y0=5; y=15; x=50; % Apartado a) Parámetro Ta syms T a=(T/w)*(cosh((w*x)/T))+y0-T/w-y; Ta=solve(a,T) % Apartado b) Longitud del cable x1=150; L=(2*Ta/w)*sinh(2*w*x/Ta)
Warning: Cannot solve symbolically. Returning a numeric approximation instead. Ta = 1266.324360399888280635385997007 L = 221.44470407313733923826840058546